Econophysicist Predicts Date of Chinese Stock Market Collapse–Part III
First came the prediction, then the prediction came true. Now the econophysicist explains how he did it.
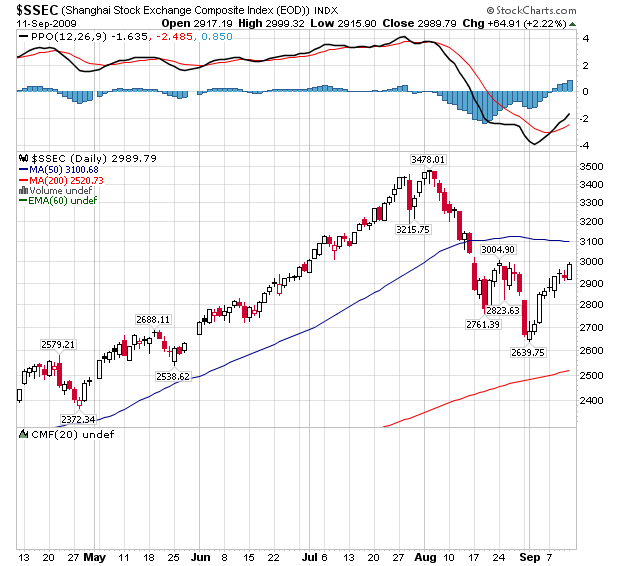
Back in July, econophysicist Didier Sornette at the Swiss Federal Institute of Technology in Zurich and a few pals predicted the impending collapse of the Shanghai Composite stock market index.
Their evidence was that the index had been growing at a faster than exponential rate, which was clearly measurable and obviously unsustainable. But Sornette and co were less forthcoming about how they were able to say a collapse was imminent. I was sceptical of this prediction and said so.
And yet at the beginning of August, the Shanghai Composite dropped by about 20 per cent and I was forced to eat my words, puzzled though I still was to their method.
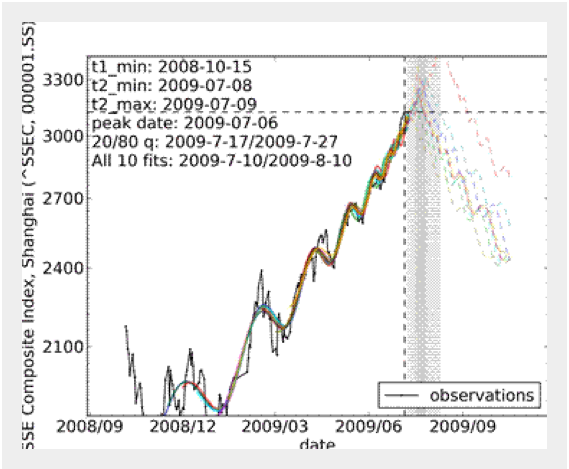
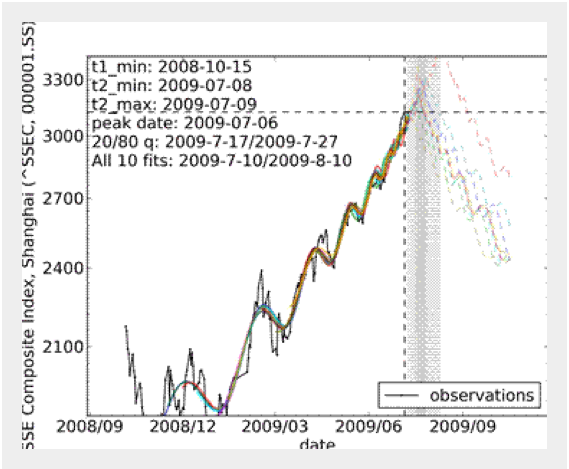
Today, Sornette and co publish the method they use to make their prediction. Their method is a synthesis of ideas from the economic theory of rational expectation bubbles, from the imitation and herding behaviour of investors and traders and from the mathematical and statistical physics of bifurcations and phase transitions.
From this, they say they have discovered an unambiguous signature of a bubble market about to collapse in the form of super-exponential growth decorated with logarithmic oscillations as in the diagram above.
Sornette says he has used this method to predict the collapse of several bubbles in the last few years, including the collapse of the oil bubble last year and the US housing market in 2006.
That’s important work which could have a profound impact on economic models. If Sornette and his colleagues have put their money where there mouths are, they ought to be super rich by now.
One interesting aspect of Sornette’s predictions is that the team claim that they will not affect the market in a way that changes the forecast.
“Even in the presence of investors fully informed of the presence of the bubble and with the knowledge of its end date, it remains rational to stay invested in the market to garner very large returns since the risk of a crash remains finite.”
Of course, the end of a bubble doesn’t always imply a crash, just a change from super exponential growth to some other kind of market dynamics.
But if Sornette’s forecasts prove reliable, the herding behaviour of traders and investors makes it seem inevitable that they will trigger crashes. If that happens, they will become self-fulfilling prophecies that will generate some interesting dilemmas for traders and regulators alike.
Ref: arxiv.org/abs/0909.1007: Bubble Diagnosis and Prediction of the 2005-2007 and 2008-2009 Chinese stock market bubbles
By combining (i) the economic theory of rational expectation bubbles, (ii) behavioral finance on imitation and herding of investors and traders and (iii) the mathematical and statistical physics of bifurcations and phase transitions, the log-periodic power law model has been developed as a flexible tool to detect bubbles. The LPPL model considers the faster-than-exponential (power law with finite-time singularity) increase in asset prices decorated by accelerating oscillations as the main diagnostic of bubbles. It embodies a positive feedback loop of higher return anticipations competing with negative feedback spirals of crash expectations. We use the LPPL model in one of its incarnations to analyze two bubbles and subsequent market crashes in two important indexes in the Chinese stock markets between May 2005 and July 2009. Both the Shanghai Stock Exchange Composite and Shenzhen Stock Exchange Component indexes exhibited such behavior in two distinct time periods: 1) from mid-2005, bursting in Oct. 2007 and 2) from Nov. 2008, bursting in the beginning of Aug. 2009. We successfully predicted time windows for both crashes in advance with the same methods used to successfully predict the peak in mid-2006 of the US housing bubble and the peak in July 2008 of the global oil bubble. The more recent bubble in the Chinese indexes was detected and its end or change of regime was predicted independently by two groups with similar results, showing that the model has been well-documented and can be replicated by industrial practitioners. Here we present more detailed analysis of the individual Chinese index predictions and of the methods used to make and test them.
